Arzel utilise un ballon de basket de taille 7 pour ses compétitions. Celui-ci a une masse de 600 grammes et un diamètre de 24 cm. Le panier a un diamètre de 45 cm, et est fixé à une hauteur de 3,05 m.

Le chronomètre indique qu'il ne reste plus que 3 secondes avant la fin de la partie, et pour marquer un maximum de point, Arzel qui est à une distance de 7,63 mètres tente un panier à 3 points en tir direct.

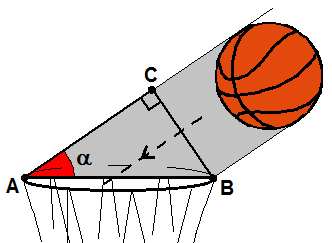
Si le tir est trop rasant par rapport au panier (angle "alpha" faible), le ballon risque de ricocher au lieu d'entrer.
Si au contraire le ballon entre dans le panier avec une trajectoire proche de la verticale, la distance parcourue depuis le joueur sera très grande et la précision du tir deviendra médiocre.

Il existe donc un angle minimal qui à la fois permet l'entrée directe dans le panier (voir figure ci-contre), et permet de garder une précision optimale. Dans la pratique le joueur utilise un angle de tir légérement plus grand pour optimiser ses chances d'entrer dans le panier.

a) Quel est le référentiel qui est utilisé pour décrire la trajectoire du ballon ?

b) A quoi correspond la distance AB ? Donnez sa valeur.

c) Même question que précédemment avec la distance BC ?

d) Quelle relation trigonométrique permet de lier l'angle alpha, AB, et BC ? Calculer alpha.

Pour la suite on supposera que l'angle d'entrée du ballon dans le panier sera de 40°. Un spectateur a enregistré la trajectoire du ballon et un logiciel d'analyse d'image nous a permis (voir figure ci-dessous) de visualiser la position de ce ballon toutes les 100 ms. Le laché intervient à la date t₀, et l'arrivée du ballon dans le panier à la date t₁₀.

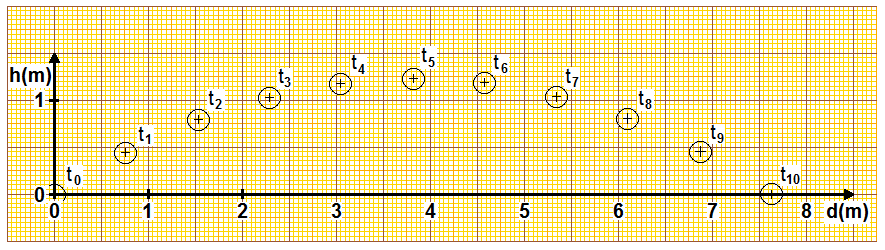
e) Calculez la vitesse instantanée du ballon à la date : t₁.

f) Calculez la vitesse moyenne du ballon entre l'instant du laché, et l'arrivée à l'entrée du panier.

g) Définir le mouvement du ballon de t₀ à t₅, puis de t₅ à t₁₀.