Mathématiques
Produit scalaire
1. Produit scalaire
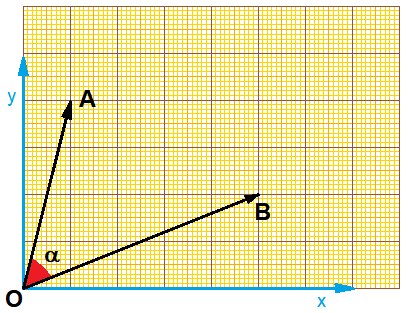
Soient les deux vecteurs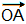 
,
, et α l'angle entre ces deux vecteurs.
Le produit scalaire est alors défini par :
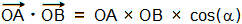
En utilisant les coordonnées des vecteurs, on a aussi :
avec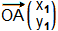 
et
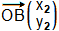
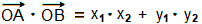
Exemple à partir de la figure :
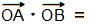1 × 5 + 4 × 2 = 13
Pour deux vecteurs définis dans un espace à 3 dimensions :
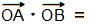x1 · x2 + y1 · y2 + z1 · z2
2. Calcul automatique d'un produit scalaire
Saisir les coordonnées des vecteurs, puis cliquez sur "Calcul".
|
|
|
|
|
|
|
·
|
||||||
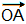Attention : Utilisez un point et non une virgule pour les nombres décimaux.
Le produit scalaire de deux vecteurs perpendiculaires est nul.