Correction

Exercice : Production du dichlore en laboratoire

1. Ecrire les demi-équations d'oxydoréduction.

Cl₂(g) + 2e^- = 2Cl^-(aq)
MnO₄^- + 8H⁺ + 5e^- = Mn²⁺ + 4H₂O

2. Ecrire l'équation complète de la réaction chimique.
Les réactifs sont placés à gauche. La première équation est multipliée par 5, et la deuxième par 2, pour permettre la suppression des électrons de l'équation complète.

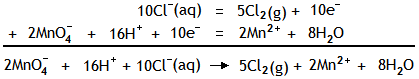
Sous cette forme, l'équation est parfaitement équilibrée, mais présente des charges globales non nulles dans chaque membre. C'est normal puisque déjà ne figure pas dans cette équation, les ions spectateurs. Ajoutons 2 ions K⁺ de chaque côté, pour retrouver notre permanganate de potassium, et aussi 6Cl^- pour équilibrer les ions H⁺ de notre acide chlorhydrique. Nous obtenons alors l'équation complète :

2KMnO₄ + 16HCl → 5Cl₂ + 2MnCl₂ + 2KCl + 8H₂O

3. On dispose de 31,6 grammes de KMnO₄.
3.a. Calculer la masse molaire du KMnO₄.

M(KMnO₄) = M(K) + M(Mn) + 4M(O) = 39,1 + 54,9 + 4 × 16 = 158 g·mol^-1

3.b. Déduire du résultat précédent la quantité de matière de KMnO₄.

n(KMnO₄) = m(KMnO₄) / M(KMnO₄) = 31,6 / 158 = 0,2 mol.

3.c. Construire le tableau d'avancement de la réaction.

	Avancement	2MnO₄^- + 16H⁺ + 10Cl^- → 5Cl₂ + 2Mn²⁺ + 8H₂O
Etat initial	x = 0	n₁	n₂	n₃	0	0	0
Etat intermédiaire	x	n₁ - 2x	n₂ - 16x	n₃ - 10x	5x	2x	8x
Etat final	x_max	n₁ - 2x_max	n₂ - 16x_max	n₃ - 10x_max	5x_max	2x_max	8x_max

On considère ici que le réactif limitant est le permanganate de potassium. Par conséquent : n₁ - 2x_max = 0
Soit encore : x_max = n₁ / 2 = 0,2 / 2 = 0,1 mol.

3.d. Quelle volume maximale de dichlore peut-on obtenir ?

n(Cl₂) = 5x_max = 5 × 0,1 = 0,5 mol.
V(Cl₂(g)) = n(Cl₂) × Vm = 0,5 × 24 = 12 Litres.